Zum Navigationspfad Unterseiten von „Lehrstuhl“ Zur Navigation Zum Schnellzugriff Zum Fuß der Seite mit weiteren Services
Zum Inhalt
Analysis LSI
Fakultät für Mathematik
Standard: Panorama Mathetower © Roland Baege​/​TU Dortmund
Angewandte Analysis (LSI)

Research

  • Porous Media: Interesting tools are needed to deal with degenerate diffusion and with hysteresis effects. Our results are on existence, approximation, and homogenization. High-light: Justification of a model for the fingering effect in porous media.
  • Plasticity: The memory effect of plastic materials makes this poblem interesting. High-light: Stochastic homogenization of plasticity.
  • Maxwell's equations: Homogenization in degenerate geometries and for large contrast materials. High-lights: Negative index meta-materials, geometric characterization of opaque materials, perfect transmission.
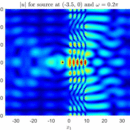
  • Helmholtz equation: Resonance effects and radiation conditions. High-light: The spectrum of small Helmholtz resonators, effective acoustic properties of a medium with many small resonators, radiation conditions in periodic media.

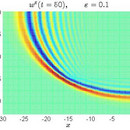
  • Wave-equation: Dispersion on large time intervals. High-light: Effective dispersive equations for wave equations in arbitrary dimension and for wave equations on lattices.

 

Other research is on elasticity and Gamma-convergence, negative index materials (cloaking), transmission conditions, optimality problems, free boundary problems, fluid mechanics.

Research in pictures

We characterize waves in lattice dynamics. The above pictureshows a ring-like wave: the initial values are concentrated in a unit ball at the origin, the lattice spacing is 1/6, the solution is shown at time 20 when the main pulse has travelled 120 lattice distances. We show that a linearized KdV-equation describes the profile of the main pulse and describe the initial values for every direction. Names: F. Theil, B. Schweizer

We derived a dispersive equation that describes the long-time behavior of waves in a heterogeneous medium. Names: T. Dohnal, A. Lamacz, B. Schweizer

We analyzed the Maxwell equations in a complex geometry that generates a meta-material with a negative index. Names: G. Bouchitte, A. Lamacz, B. Schweizer

Cloaking: Both, the ring and the small black point at position z are invisible for measurements from far away. The reason is that the ring contains a negative index material. Names: G. Bouchitte, R.V. Kohn, J. Lu, M. Weinstein, B. Schweizer

We show the existence of radiating solutions to the Helmholtz equation in unbounded periodic media with energy methods. Names: B. Schweizer

We derived effective equations that describe oil-trapping. The image shows a saturation profile in a porous medium consisting of two different materials; infinite slopes occur. Names: S. Pop, M. Ohlberger, P. Henning, B. Schweizer

We studied a hysteresis model for flow in porous media that can explain gravity fingering. Names: A. Lamacz, J. Koch, A. Rätz, B. Schweizer

What is the radiation condition (boundary condition at infinity) for the Helmholtz equation in a periodic medium? We developed one and derived a (weak) uniqueness result. We also introduced numerical schemes for an approximation of solutions. Names: T. Dohnal, A. Lamacz, B. Schweizer

Zum Seitenanfang